Do you ponder using argumentation software such as Argunet, but have not taken a course in argumentation theory or logic yet? Or do you just want to refresh you argument analysis skills? There’s plenty of learning material on the web that helps you to improve you critical thinking skills. This post features and comments on three free online courses.
- OLI: A course on argument diagramming by the Open Learning Initiative (OLI) at Carnegie Mellon University.
- CTW: The Critical Thinking Web compiled by Joe Lau and Jonathan Chan, hosted by the Philosophy Department at Hongkong University.
- AUT: The Argument Mapping Tutorials by Austhink.
My upshot: If you’re a newbie to argument analysis and look for a steady, step-by-step introduction, you should start with OLI‘s course and then move to the Criticial Thinking Web for more specific details and thorough treatments. In case you prefer a crisp and astute introduction, you may skip OLI and start directly with browsing the CTW (especially Module A). These two online courses jointly teach you as much as a good critical thinking textbook does. Once you have a firm grip on the topic of argument reconstruction, you might want to check out what Austhink‘s argument mapping tutorials have to say on reconstructing complex debates that consist in many arguments.
Illustrative Reconstructions
Let’s have a look at representative argument reconstructions from the tutorials, which give you a flavour of the different approaches. (My comments are cast against the background of the reconstruction ideal spelled out here.)
OLI’s Argument Diagramming Course
The Argument Diagramming Course discusses a couple of complex arguments, for example the following one:
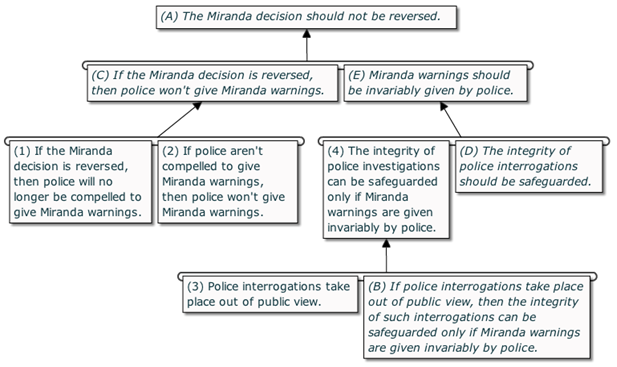
If the Miranda decision is reversed, police will no longer be compelled to give those warnings; and if they aren’t compelled to give them, they won’t give them. But because police interrogations take place out of public view, the integrity of such interrogations can be safeguarded only if those Miranda warnings are invariably given.
The argument is reconstructed as follows (standard form):
Premise: (1) If the Miranda decision is reversed, then police will no longer be compelled to give Miranda warnings.
Premise: (2) If police aren’t compelled to give Miranda warnings, then police won’t give Miranda warnings.
Implied Sub-conclusion: (C) If the Miranda decision is reversed, then police won’t give Miranda warnings.
Premise: (3) Police interrogations take place out of public view.
Implied Premise: (B) If police interrogations take place out of public view, then the integrity of such interrogations can be safeguarded only if Miranda warnings are invariably given by police.
Sub-conclusion: (4) The integrity of police interrogations can be safeguarded only if Miranda warnings are invariably given by police.
Implied Premise: (D) The integrity of police interrogations should be safeguarded.
Implied Sub-conclusion: (E) Miranda warnings should invariably be given by police.
Main conclusion: (A) The Miranda decision should not be reversed.
And it is visualized as an argument diagram:
Comment: I think that’s nearly perfect. As you can see, the individual inferences are valid and the argument reconstruction hence makes explicit the hidden (“implied”) assumptions of the original reasoning.
Critical Thinking Web
The following text is analysed on the Critical Thinking Web.
We should not inflict unnecessary pain on cows and pigs. After all, we should not inflict unnecessary pain on any animal with consciousness, and cows and pigs are animals with consciousness.
CTW reconstruct the argument as:
(Premise 1) We should not inflict unnecessary pain on any animal with consciousness.
(Premise 2) Cows and pigs are animals with consciousness.
(Conclusion) We should not inflict unnecessary pain on cows and pigs.
Comment: While CTW covers a broad range of topics in logic and argumentation theory that are highly relevant for argument reconstruction, it is, in the same time, a bit poor on (sufficiently complex) examples. — But otherwise the argument reconstructions in CTW, as the one above, are impeccable.
Austhink’s Argument Mapping Tutorials
Now compare how Austhink treats arguments.
The shadows of the astronauts and their equipment in the Apollo pictures seem to point in different directions. This suggests that artificial lighting was used and therefore the pictures were taken in a studio on earth.
This piece is reconstructed as follows.
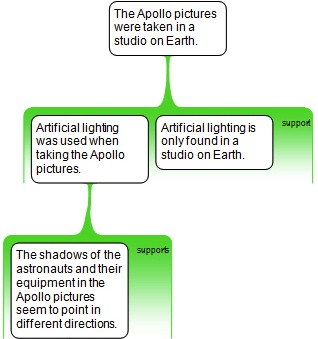
Comment: Depending on how you spell out the logico-semantic structure of the premisses, the first inference (from middle layer to top conclusion) might be valid, but the second inference clearly isn’t. Many Austhink reconstructions seem to lack the level of precision and explicitness I tend to aim at. (One reason might be that various issues like, e.g., ambiguity can be illustrated with invalid or incomplete reconstructions, too. Nonetheless, the tutorials clearly don’t emphasize explicitness and inferential correctness as much as the OLI course and CTW do.)
How the courses relate to Argunet — and some further remarks
- Argument map — one word, many things. All courses explain how to create argument diagrams. In the first place, these diagrams visualize the internal (inferential) structure of a single argument. The nodes in these diagrams are statements (and not entire arguments or reasons). So, these argument diagrams translate, in Argunet, into detailed reconstructions you’d compile with the argument editor and represent in standard form (i.e., as a list; more on translating argument diagrams to Argunet here). Accordingly, the argument diagrams are not to bo confused with Argunet argument maps, which contain (primarily) entire arguments as boxes and which visualize the dialectical structure of a debate.This is the reason why Austhink’s recommendation “No Reasoning in Boxes” does not apply to Argunet. (It is however correct that a single premiss in an argument, reconstructed in Argunet, should not contain an inference.)
- Truth tables. The OLI course and the Critical Thinking Web use the truth table method for checking whether (simple) arguments are deductively valid. That is, I believe, inadequate and risks to lead beginning argument analysts astray. To see this, consider the following argument:
- If Peter publishes the original paper even though his student has shown it to be flawed, then Peter is a poor scientist.
- Peter’s student has not shown Peter’s paper to be flawed.
- Thus: Peter is a poor scientist.
This is a very bad argument. The conclusion does apparently not follow from the premisses (it can be false while the premisses are true). Now, the argument may be formalized as follows:
- If (if P then Q) then R.
- Not P.
- Thus: R.
And the truthtable method yields that this inference is deductively valid. So the truthtable method gives wrong results and may lead us astray.
That’s why I don’t teach truth tables in my argumentation courses anymore.
(The problem arises, of course, in the formalization of the conditional in premiss (2). If you reconstruct it as a strict implication (in terms of modal logic), for example, the conclusion does not follow anymore and logic gives you the right result, again. However, the problem is that OLI and CTW invite us to use propositional logic and, specifically, truth tables in an uncritical way, and that’s what’s highly problematic.)
- Rules of thumb. The Austhink tutorial #2 establishes a couple of rules of thumbs for argument reconstruction. These, I think, should be relaxed. Contrary to the Golden Rule, for example, there exist excellent arguments with just one premiss (e.g., arguments that provide a counterexample to a universal statement). Moreover, rather than using rules of thumb for identifying hidden assumption, I strongly recommend to unearth implicit premisses against the background of a validity check (as described by CTW).
- The macrostructure of debate. What distinguishes the Austhink tutorials from OLI and CTW is that they discuss the macrostructure of a debate reconstruction. This is certainly interesting and valuable. I only find that the pyramid rule cannot be applied to reconstructions created with Argunet (and I doubt it’s a good rule when you work with other argument mapping software). There’s simply no reason to think that the generality of a claim or argument is correlated with its dialectic location in a debate. Arguments that rely on highly general principles can both be raised at the centre as well as at the outskirts of a controversy; very special claims (pieces of evidence, counterexamples) can bear directly on the central thesis or concern outward arguments.

Comments are closed.